The Isosceles Triangle Problem

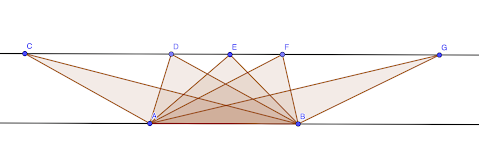
The lines below are parallel. 

If we place a point on the top line, we can connect that point to points A and B to create an isosceles triangle:  (Remember -- an isosceles triangle has two sides of the same length.)

Question:  How many other ways can this be done?  How many distinct isosceles triangles can you make that include points A and B as two of the three vertices?

For the solution, click "Read More" below.

Solution:

There are five distinct isosceles triangles that include A and B as vertices.

In triangle ABC, sides AB and AC are congruent.

In triangle ABD, sides AB and DB are congruent.

In triangle ABE, sides AE and BE are congruent.

In triangle ABF, sides AB and AF are congruent.

In triangle ABG, sides AB and BG are congruent.