Why can't I divide by zero?

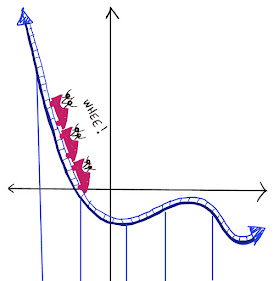
What is 4 divided by zero?  Some students reason that you can think of it as long division and take out as many zeroes as you like from 4 without ever making 4 smaller.  So maybe 4 divided by zero is "infinity"?

That's not unreasonable.  In fact American textbooks from the 1800s took that point of view.  The image below is from the 1876 edition of Charles Davies algebra textbook, p. 83. He says that a number divided by zero is equivalent to infinity.

The problem with dividing by zero is that it leads to contradictions. If 4 divided by zero is "infinity," then does that mean that infinity times zero equals 4?  

Check out this sweet little song about Zero, which shows the problem.  Zero is powerful, but it is also dangerous. If you are not careful when you divide, you might run into contradictions. You might even break math! Link to video is here.

Rectangles and Triangles

Rectangles are so simple.  Their angles are always 90 degrees.  But triangles come in all different shapes. So how do you find the area of a triangle?  

Check out this musical video about the area of triangles:  Rectangles and Triangles

Map Folding Problem

The lines in the map above show how it was folded.  Dotted lines show a “valley fold” and solid lines show a “mountain fold.”  This map was folded in half horizontally, then vertically, then vertically again.

Question:  Each of the maps below was folded in four steps – in half each time.  Which of the maps is an “impossible map”?

Also check out my new project: musical math videos. Subscribe to the YouTube Channel to get more as they are released!

For the solution to the map problem, click here:

Prime Time!

A new song!

Welcome to Prime Time Building Supply! Imagine a store  that sells prime numbers. We sell classics like 2, 3, 5, or 7. We also sell the elegant and understated 1009. With our prime numbers, you can build composite numbers of any size!

The song:  Prime Time

Gauss’ Trick

I am happy to announce the launch of a new project. This is the first in a series of musical math videos. Please enjoy and share this song about the mathematician Gauss as a little boy and his trick for adding the numbers from 1 to 100.  

Musical video:  https://youtu.be/XlGsUlIEdYc

Companion video explanation of Gauss' method:  https://youtu.be/fTluDWc1v-A

Lattice Polygons, Part 2

Lattice polygons are polygons are formed by connecting dots on square dot paper.  (On a coordinate graph, the coordinates of the vertices are integers.). 

The lattice polygon below is a rectangle whose dimensions are 2 units by 4 units.  Its area is 8 square units.

(1)  Can you make a small change to the rectangle so that the area of the new polygon is 6 square units? There are lots of ways to do this.

(2)  How many different kinds of polygons can you make on a geoboard with an area of exactly 6 square units?  Can you make a triangle?  a quadrilateral?  a 5-sided figure?  6-sided?  7-sided?  8-sided?

It is convenient to use this online geoboard:  Geoboard

For the solution, click below:

Same Sum Circles, Part 2

The goal of this puzzle is to place the numbers 1 through 7 in the circles so that you get the same sum in each circle.  

Notice that the placement below is ALMOST a solution but not quite.  One circle has a sum of 17 and the other two have a sum of 19.  You can fix it by moving only one bean.  Which one?  Where would you move it?

Once you figure that out, see how many different sums you can make.  You can make quite a lot!

Click "read more" for the solution:

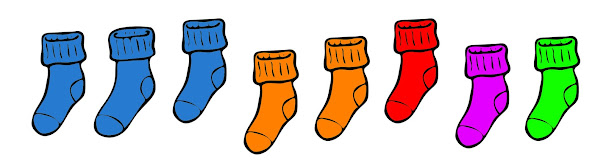
The Sock Problem #2

Silas reaches into his sock drawer in the dark, and he wants to make sure that he grabs a matching pair.  The drawer has 3 identical blue socks, 2 orange, 1 red, 1 purple, and 1 green sock. 

Question:  How many socks must Silas grab to ensure that he has at least one matching pair? 

For the solution, click "read more" below: